[hp15c]

HP15c program: quadratic equation solver, x2+p*x+q=0

This program uses only the stack (no storage registers) and it works for complex numbers. 
command         display

f LBL C        001-42,21,13
   x><y         002-      34
   2            003-       2
   CHS          004-      16
   ÷            005-      10
   Enter        006-      36
   *            007-      20
g LST X        008-43    36
g LST X        009-43    36
   R_arrow_down 010-      33
   R_arrow_down 011-      33
   x><y         012-      34
   -            013-      30
   square root  014-      11
   R_arrow_down 015-      33
g LST X        016-43    36
   square root  017-      11
   -            018-      30
   x><y         019-      34
g LST X        020-43    36
   +            021-      40
g RTN          022-   43 32

Re-number program code starting with line number:

This program uses the following label: LBL C

Using the program

I start every program with a label. This way you can have a number of programs in your 15c and you just select which one to run by pressing f LABELNAME (f C in this case) or GSB LABELNAME (GSB C in this case).

This program finds the points x1 and x2 on the X-axis where the graph y=x2+p*x+q intersects with the X-axis.


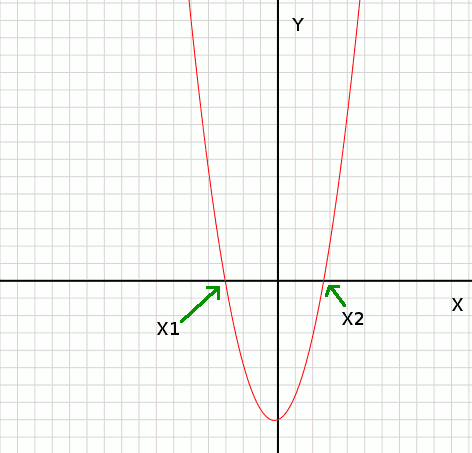
graph: y=x2+p*x+q

Quadratic equation: x2 + 0.5*x - 3=0
Roots: x2= 1.5 and x1= -2
The number in front of the x of the equation (called p further up) goes into y register of the stack and q goes into the x register of the stack (the x register is equal to the display line).
You type: 0.5, ENTER, 3, CHS, GSB C
The display shows "running" and then you see 1.5. This is one solution and you see the other one by pressing the "x><y" (swap x and y stack registers): x2=1.5 x1=-2

Here is a test equation for complex numbers: x2 -5i*x -6 = 0
Roots: x2= 3i and x1= 2i
You enter the complex numbers 0-5i and -6+0i as follows: 0, ENTER, 5, CHS, f I, 6, CHS, run the program with: GSB C
As solutions you should get 0 + 3i and 0 + 2i. So after running the program you will just see zero in the display. To see the full complex number you type and hold f (i). This shows the imaginary part as long as you hold the button. Release the button and type "x><y" (swap x and y stack registers) to see the second solution. It's also zero but the imaginary part is 2 (see with f (i) ).

Here is another a test equation for complex numbers: x2 -16*x +89 = 0
Roots: x2= 8 + 5i and x1= 8 - 5i
This equation has no solution in normal mode. You will get Error 0 if you are not in complex mode. But if you activate complex mode with "g SF, 8" (display shows a "c" on the right side of the display) then you will get the solutions: 8 + 5i and 8 - 5i.

It is possible that the quadratic equation has no solution (if you move the parabola above the X-axis such that there is no intersection with the X-axis). In this case you will see "Error 0" in the display.

HP11C

This program works without changes on the HP11c however the HP11c does not have complex numbers and therefore the program can not find complex roots.

Algorithm for solving and factorizing a quadratic equation

x2 + p*x + q=0 has the following 2 solutions:

x1=-p/2 - sqrt((p/2)2 - q)
x2=-p/2 + sqrt((p/2)2 - q)

The quadratic equation can also be written in its factored from
with x1 and x2 as shown above:
x2 + p*x + q = (x - x1)*(x - x2)


Note that the HP15c has as well the f SOLVE function but this program is useful if you have to solve quadratic equations frequently. SOLVE can also not find complex roots.

Javascript quadratic equation solver

Quadratic equation:
x2 + p*x + q=0
 or 
in the factorized form:
x2 + p*x + q = (x - x1)*(x - x2) = 0
where 
 p=-(x1 + x2)
  and
 q=x1 * x2

Please enter p and q (note a limitation of this javascript code is that p and q can not be complex numbers):

x2 + *x + = 0



Please turn on JavaScript!

Result (x values where the curve hits the x-axis):
x1=
x2=



© Guido Socher