home |
science club |
tuxtalk |
photos |
toolbox |
avr microcontroller & DIY electronics |
e-cards |
familyhistory

no preservatives added blog |
computer and graphics corner |
herbal treasure chest |
splash into math |
periodic table
multiplication trick for 2 numbers between 6 and 9
Gini and Karl discover the "Double-Hand" Multiplication Trick
One snowy morning at the Penguin Café, Karl was staring at the menu board.
"Why are the numbers between 6 and 9 always the hardest to multiply?" he groaned.
Gini looked up from her cocoa.
"Then let's use both flippers."
She placed her hands next to each other on the table, fingers facing inward, just like mirror images.
"Today," she said, "we're counting from 6 to 10."
They numbered their fingers:
bottom finger: 6
then 7, 8, 9
top finger: 10
Flip, Pip, and Flipflop leaned closer.
Step 1: Lining Up the Fingers
"Let's try 8 * 7," Karl suggested.
Gini lined up the finger marked 8 on her left hand with the finger marked 7 on her right hand so they faced each other.
"Now comes the fun part," she said.
They counted:
the two fingers touching
and all the fingers below them
Each counted finger was worth 10.
Karl counted aloud:
left hand: 3 fingers → 30
right hand: 2 fingers → 20
"Together that's 50," he said.
Step 2: The Fingers on Top
Gini pointed to the fingers above the touching ones.
"Now count what's left on top."
left hand: 3 fingers
right hand: 2 fingers
They multiplied them:
3 * 2 = 6
Step 3: Put It Together
"Last step," said Gini.
"Add both results."
50 + 6 = 56
Karl blinked.
"So 8 * 7 = 56... and we didn't write anything down!"
They kept going.
7 * 7
tens: 20 + 20 = 40
top fingers: 3 * 3 = 9
→ 49
8 * 8
tens: 30 + 30 = 60
top fingers: 2 * 2 = 4
→ 64
7 * 9
tens: 20 + 40 = 60
top fingers: 3 * 1 = 3
→ 63
Even Penguin Waddle tried it (very carefully).
Walter the dolphin tried too... with fins. Results were impressive but unofficial
Flipflop cleared his throat.
"This looks like magic," he said, "but it's really algebra wearing a penguin costume."
He grabbed a napkin.
"Let's call our numbers x and y."
"When we count fingers from 6 up to x, we're really counting
x - 5 fingers."
Gini nodded.
"Because we started at 6, not at 1."
"And each of those fingers counts as 10," Flipflop continued.
"So step one is:
10*(x - 5) + 10*(y - 5)
or
10*((x - 5) + (y - 5))"
Karl scribbled little flippers next to the formula.
"Next," said Flipflop,
"we count how many fingers are left up to 10."
"That's
10 - x and 10 - y."
"And when we multiply those fingers," Gini added,
"we're really calculating:
(10 - x)*(10 - y)"
"To get the final answer," Flipflop said,
"we add both parts together."
10*(x - 5) + 10*(y - 5) + (10 - x)(10 - y)
He simplified it step by step, and suddenly...
"Everything cancels," Karl whispered.
Flipflop smiled and tapped the napkin.
"Only x*y is left."
q.e.d.🎩
Chef Pebble applauded from behind the counter.
"So the hands were doing the algebra all along."
Gini wiggled her fingers.
"Turns out, math has been right at our flipper-tips."
And from that day on, whenever numbers between 6 and 9 appeared at the Penguin Café,
Gini and Karl didn't panic.
They just held out their hands —
and let the math line itself up.
Now here is the trick again with pictures:
First you put your hands next to each other with the fingers facing each other (like in the picture). Number your fingers from 6 to 10, starting with 6 at the bottom and ending with 10 at the top.

Align your fingers such that the fingers with the numbers you want to multiply directly face each other. Let's take 8*7 as our example.
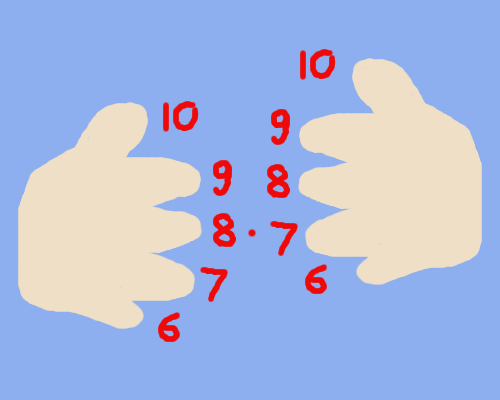
Next we count the fingers that face each other as well as all the fingers below in steps of ten.
In our example of 8*7 we count 10+10+10 = 30 on the left hand and 10+10=20 on the right hand. Together this is 30+20=50. (step1)
Now you count the remaining fingers (the fingers on top of the fingers that face each other) of the left hand and multiply that number with the number of the remaining fingers of the right hand.
In our example that is 3*2=6. (step2)
To get the result of the multiplication you wanted to calculate you add the two results you got together, that is in our example 50+6=56. (step3)
Let's try it for 7*7:

Aligning your fingers and then counting the fingers that are facing each other plus the ones below in steps of ten you get 20+20=40.
For the fingers on top you get 3*3 = 9
Add the two results together and you get 49.
Let's try 8*8:

Aligning your fingers and then counting the fingers that are facing each other plus the ones below in steps of ten you get 30+30=60.
For the fingers on top you get 2*2 = 4
Add the two results together and you get 64.
Let's try 7*9:

Aligning your fingers and then counting the fingers that are facing each other plus the ones below in steps of ten you get 20+40=60.
For the fingers on top you get 3*1 = 3
Add the two results together and you get 63.
You can see that the method is working by looking at the algebra behind it.
Let's call our two numbers x and y, that is we want to solve x*y.
Let's try to express what we did with our hands in algebraic form.
We first count the fingers on one of our hands from 6 to x. That is the same as writing x-5.
(I hope you can see that it is the same. We need to subtract 5 as we don't count from 1 but from 6 only)
We do the same with the other hand and get y-5.
We actually counted in steps of 10 which is the same as multiplying our result by 10.
So we can write 10*(x-5) + 10*(y-5) (step1)
(or 10*((x-5) + (y-5)) which by using the distributive law a*(b+c) = a*b + a*c is the same).
Next we counted the fingers from our number to 10 on each hand and multiplied them with each other.
To get to this number we can write 10-x and 10-y respectively.
(Think about what we did, we counted from our number up to 10 which is the same as finding the difference between 10 and our number, or subtracting our number from 10)
Next we multplied the counted numbers:
(10-x)*(10-y) (step 2)
To get the result we are looking for we then needed to add our 2 results together (step3):
10*(x-5) + 10*(y-5) (from step1) + (10-x)*(10-y) (from step 2)
Now we only need to simplify this expression a bit:
10*(x-5) + 10*(y-5) + (10-x)*(10-y) <==>
10x -50 +10y -50 +100 -10y -10x +xy <==>
100 - 50 -50 + 10x - 10x + 10y - 10y + xy <==>
xy
q.e.d. (quod erat demonstrandum = what was to be shown)
references
http://mathandmultimedia.com/2011/04/23/finger-math-multiplication
http://mathandmultimedia.com/2011/05/12/why-finger-multiplication-works
Copyright © 2004-2026 Katja Socher, tuxgraphics.org






